3987. Complete graph

An undirected graph is called complete, if any pair of distinct vertices is connected by at least one edge. Given a list of graph edges, check whether the graph is complete.

Input. The first line contains the number of vertices n (1 ≤ n ≤ 100) and the number of edges m (1 ≤ m ≤ 10⁴) in the graph. Then m pairs of numbers are given, representing the graph edges.

Output.  Print “YES” if the graph is complete and “NO” otherwise.

Sample input	Sample output
3 3 1 2 1 3 2 3	YES

SOLUTION

graphs

Algorithm analysis

Let А be the adjacency matrix. A graph is complete if all cells in matrix A (except the diagonal elements) contain ones.

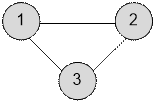
Example

Graph given in a sample, has a form:

Algorithm realization

The adjacency matrix is stored in the array g.

#define MAX 101

int g[MAX][MAX];

Read the input data. Create the adjacency matrix.

scanf("%d %d",&n,&m);

memset(g,0,sizeof(g));

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a][b] = g[b][a] = 1;

}

Iterate over the elements of the matrix, located above the main diagonal. If all of these elements are equal to 1, then at the end of the loop, the variable flag will contain 1. If at least one element of the matrix is 0, then the graph is not complete, and flag should be set to 0.

flag = 1; // complete graph

for(i = 1; i <= n; i++)

for(j = i + 1; j <= n; j++)

if (g[i][j] == 0) flag = 0;

Print the answer.

if (flag == 1) puts("YES");

else puts("NO");

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

int g[][] = new int[n+1][n+1];

for(int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

int res = 1;

for(int i = 1; i <= n; i++)

for(int j = i + 1; j <= n; j++)

if (g[i][j] == 0) res = 0;

if (res == 1)

System.out.println("YES");

else

System.out.println("NO");

con.close();

}

}

Python realization

Read the number of vertices n and the number of edges m in the graph.

n, m = map(int, input().split())

Read the adjacency list. Create the adjacency matrix g.

g = [[0] * (n + 1) for _ in range(n + 1)]

for _ in range(m):

a, b = map(int, input().split())

g[a][b] = g[b][a] = 1

Iterate over the elements of the matrix, located above the main diagonal. If all of these elements are equal to 1, then at the end of the loop, the variable flag will contain 1. If at least one element of the matrix is 0, then the graph is not complete, and flag should be set to 0.

flag = 1

for i in range(1, n + 1):

for j in range(i + 1, n + 1):

if g[i][j] == 0: flag = 0

Print the answer.

if flag == 1: print("YES")

else: print("NO")